[List of posts | playground | source code for this post]
So far in this series we've focussed on creating mazes on rectangular grids. In fact, the first two algorithms we came across (Binary Tree and Sidewinder) explicitly rely on a rectangular grid, because they give special meaning to the four cardinal directions (North, South, East and West).
However, the eagle-eyed among you might have noticed that the Recursive Backtracker algorithm (which we covered last time) only relies on being able to determine which pairs of cells are neighbours. So in this post, we're going to apply the Recursive Backtracker algorithm to a hexagon grid.
Perhaps this is a bit of a spoiler, but I think the results are really cool so I'm going to show you one now!
Refactoring
Before we implement a maze on a hexagon grid, we'll need to do some refactoring.
I'd imagine that most of my readers will know what that means, but for those that don't know here's a quick definition: refactoring means changing the structure of code without changing its behaviour. For example, you might change the name of something in your code and update all the references to it to use the new name. Nothing has changed about what your code actually does, but the way it gets to the result has changed.
In our case, our Maze class is tied to the notion of cells within a
rectangular grid. We need to make it more generic, so that it can be applied to
any type of cell.
I won't bore you with all of the details (you can go and look at the commits if you like), but the key change was to define the maze in terms of adjacency; that is, which pairs of cells are neighbours. Previously the maze was defined in terms of which walls each cell had, which limited me to a rectangular grid. I also changed the code for the Recursive Backtracker algorithm to be generic in the same way.
Hexagon grids
Now all we need to do is create some types to model a hexagon grid.
My entire understanding of how to implement hexagons in code comes from this excellent guide by Red Blob Games. I won't be able explain things any better here, so instead I'll just show you my code.
We have a type to represent a cell in a hexagon grid. I've chosen to use cube coordinates, represented here with the letters q, r and s.
public record HexCell
{
public HexCell(int q, int r, int s)
{
if (!CoordinatesValid(q, r, s))
{
throw new ArgumentException("q, r and s must sum to zero");
}
this.Q = q;
this.R = r;
this.S = s;
}
public int Q { get; }
public int R { get; }
public int S { get; }
public int DistanceFromOrigin => Coordinates.Select(Math.Abs).Max();
public static bool CoordinatesValid(int q, int r, int s) => q + r + s == 0;
public HexCell GetNeighbourInDirection(HexDirection direction) =>
new(Q + direction.Q, R + direction.R, S + direction.S);
}We have a type representing the adjacency directions within a hexagon grid.
public record HexDirection
{
private HexDirection(int q, int r, int s)
{
this.Q = q;
this.R = r;
this.S = s;
}
public static HexDirection NorthEast { get; } = new(1, -1, 0);
public static HexDirection East { get; } = new(1, 0, -1);
public static HexDirection SouthEast { get; } = new(0, 1, -1);
public static HexDirection SouthWest { get; } = new(-1, 1, 0);
public static HexDirection West { get; } = new(-1, 0, 1);
public static HexDirection NorthWest { get; } = new(0, -1, 1);
public static IEnumerable<HexDirection> GetAll() =>
[
NorthEast,
East,
SouthEast,
SouthWest,
West,
NorthWest,
];
public int Q { get; }
public int R { get; }
public int S { get; }
}We also need a type to represent the grid itself. I've chosen to define the grid in a radial fashion, including an origin at the centre and all cells up to a specified distance away from the origin.
public class HexGrid
{
public HexGrid(int maxDistanceFromOrigin)
{
this.MaxDistanceFromOrigin = maxDistanceFromOrigin;
var cells =
from q in RangeBetweenInclusive(-maxDistanceFromOrigin, maxDistanceFromOrigin)
from r in RangeBetweenInclusive(-maxDistanceFromOrigin, maxDistanceFromOrigin)
from s in RangeBetweenInclusive(-maxDistanceFromOrigin, maxDistanceFromOrigin)
where HexCell.CoordinatesValid(q, r, s)
select new HexCell(q, r, s);
this.Cells = cells.ToList();
}
public int MaxDistanceFromOrigin { get; }
public IReadOnlyList<HexCell> Cells { get; }
public IEnumerable<HexCell> GetNeighbours(HexCell cell) =>
from direction in HexDirection.GetAll()
let neighbour = cell.GetNeighbourInDirection(direction)
where this.IsWithinBounds(neighbour)
select neighbour;
private static IEnumerable<int> RangeBetweenInclusive(int lowerBound, int upperBound) =>
Enumerable.Range(lowerBound, upperBound - lowerBound + 1);
public bool IsWithinBounds(HexCell cell) => cell.DistanceFromOrigin <= this.MaxDistanceFromOrigin;
}Drawing a hexagon grid mostly comes down to knowing where the vertices of each cell are. For this I refer you again to the the article by Red Blob Games (seriously, go and read it!). The code for this is in HexMazeImage.cs (it's quite long, so I won't reproduce it here).
Here's what the grid looks like if you set the size to 6.
Generating hexagon mazes
At this point, it's just a case of combining the code we already have for the Recursive Backtracker algorithm with the code defining hexagon grids.
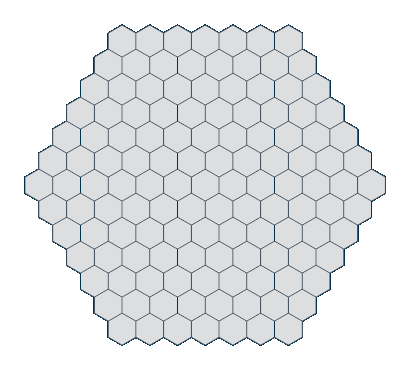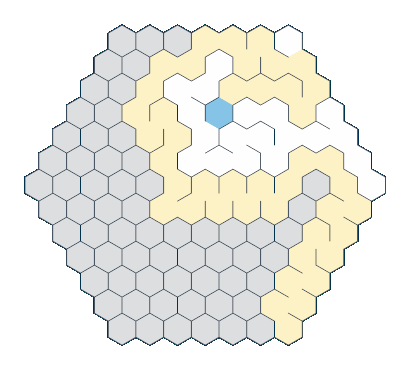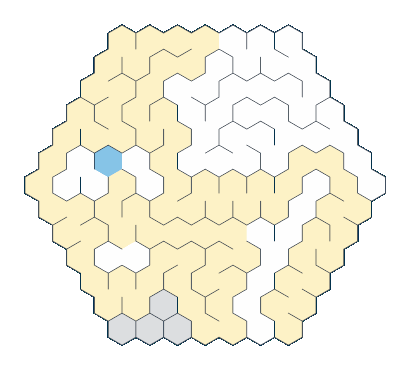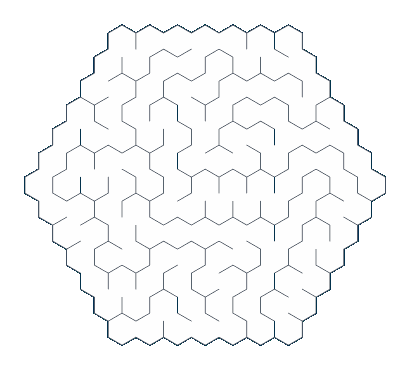
Here's what you end up with. I think the results are great!
Conclusion
When I started this blog series one of my aims was to generate visually appealing images (the other being to do it using as much functional code as possible). I'm really pleased that these hexagon mazes have come out looking so cool, and it's given me motivation to continue with this series and see what I can create!
Up next: I'm not entirely sure at the moment! I've got some ideas for other types of mazes, but I'd also like to explore procedurally generating other structures. Watch this space ...

