ProcGen Fun 6: The Recursive Backtracker algorithm

[List of posts | playground | source code for this post]

The animation below demonstrates the inner workings of the Recursive Backtracker algorithm for maze generation.

You can probably figure out how it works just by watching this animation. However, in this post I'll give a more detailed example, define the algorithm precisely, and then implement it in C#.

Example

Let's use a smaller grid for our example.

To start with, pick a cell at random.

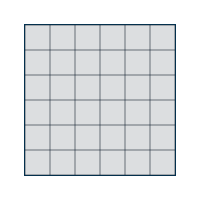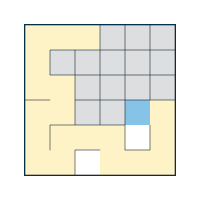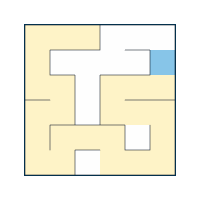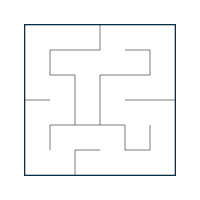
Then pick one of its neighbours at random, remove the wall in that direction, and move to this as your new current cell.

I'm using blue for the current cell, and light yellow for the cells we've already visited.

Repeat the process with the new current cell: pick a random neighbour and move to it, this time making sure you haven't visited that cell before.

Repeat the process, each time picking a random unvisited neighbour and moving to it.

Eventually you'll end up in a situation where you're fenced in and you've already visited all of the current cell's neighbours.

If this happens, retrace your steps to the previous cell.

I'm using white to denote the cells which we won't need to visit again.

Continue with the same rules: if there's an unvisited neighbour then randomly pick one and move to it; otherwise, retrace your steps.

In this case, we have a neighbour we can move to.

Eventually, all the cells will have been visited.

At this point, keep following the same rules, and retrace your steps all the way back to the beginning.

Here's this example as a full animation.

The algorithm

Now we've seen an example, here's a more precise definition of the Recursive Backtracker algorithm.

As you go through the process, keep track of the following pieces of state.

• Which cell walls are present
• The current cell
• The path you took to get to the current cell
• Which cells have been visited

Here's the algorithm.

1. Start with all the cell walls present, and pick a current cell at random.
2. Identify whether the current cell has any unvisited neighbours.
   • If so, add the current cell to the path, pick one of the unvisited neighbours at random to be the new current cell, and remove the wall between the previous and new current cells.
   • If not, remove the most recently visited cell from the path and make it the current cell.
3. Repeat step 2 until all the cells have been visited and the path is empty.

What I love about this algorithm is that it's so intuitive. You can imagine that the maze grid is a set of brick walls and you're walking through it with a sledgehammer, leaving a trail of breadcrumbs along the way!

Random walks

Before I get to the implementation of Recursive Backtracker, I'd like to take a short detour to discuss random walks. A random walk is a sequence of random steps within some state space.

That definition is a bit abstract, so let's consider an example. Suppose you draw out a number line on a piece of paper, and you place a coin on the number 0. Then you flip the coin; if it comes up heads you move it one space to the right (+1), and if it comes up tails you move it one space to the left (-1). The sequence of numbers you end up with is a random walk through the state space of integers.

The Recursive Backtracker algorithm uses a form of random walk. Instead of walking randomly between the numbers on a number line, we walk randomly around the grid until we've walked all the way back to the start and our maze is complete.

A random walk is a stochastic process which gives us a sequence of values from some state space. We can express this in code with a function which returns us a distribution of sequences of values.

public static class RandomWalk
{
    public static IDistribution<IEnumerable<T>> New<T>(
        T initial, Func<T, IDistribution<T>> stepDist) =>
        new RandomWalkDistribution<T>(initial, stepDist);

    private class RandomWalkDistribution<T>(
        T initial, Func<T, IDistribution<T>> stepDist) 
        : IDistribution<IEnumerable<T>>
    {
        public IEnumerable<T> Sample<TRng>(TRng rng)
            where TRng : notnull, IRng
        {
            var state = initial;

            while (true)
            {
                yield return state;
                state = stepDist(state).Sample(rng);
            }
        }
    }
}

We need to specify the type T whose state space we're exploring, an initial value of type T, and a function which gives us the distribution of the next step based on where we are now.

A little care needs to be taken here, as each sample from this distribution is an infinite sequence (the implementation contains a while (true) loop). However, it's pretty straightforward to limit the sequence to some finite number of values, as we'll see shortly.

We can apply this to our example with a number line and a coin. The type T will be int (representing all integers), the initial value will be 0, and we can build a distribution for the next step using a Bernoulli distribution to represent the coin toss.

IDistribution<int> StepDist(int current) =>
    from b in Bernoulli.FromRatio(numerator: 1, denominator: 2)
    let step = b ? +1 : -1
    select current + step;

var randomWalkDist = RandomWalk.New<int>(initial: 0, StepDist);

// This returns an infinite random walk.
var randomWalk = randomWalkDist.Sample(this.rng);

// Take 100 steps as an example.
var steps = randomWalk.Take(100);

Here's some sample output.

0, -1, -2, -3, -2, -1, 0, 1, 2, 1, 0, 1, 0, -1, 0, -1, 0, -1, 0,
-1, 0, 1, 0, -1, -2, -1, -2, -3, -2, -1, 0, 1, 2, 3, 2, 3, 4, 3,
2, 3, 2, 3, 2, 3, 4, 3, 4, 3, 4, 5, 6, 7, 6, 5, 6, 7, 6, 5, 4, 5,
4, 3, 2, 1, 0, -1, 0, 1, 2, 3, 2, 3, 4, 3, 2, 1, 0, -1, 0, 1, 2,
1, 0, -1, -2, -1, 0, -1, 0, 1, 0, 1, 2, 3, 2, 1, 2, 1, 0, -1

Implementing Recursive Backtracker

Now we have the ability to generate random walks, we have enough to start implementing Recursive Backtracker.

We need to be able to calculate the neighbours of any given cell, so let's add a little code to the grid for that.

public record Neighbour(Cell Cell, Direction Direction);

public class Grid
{
    private static readonly IEnumerable<Direction> AllDirections =
        [Direction.North, Direction.East, Direction.South, Direction.West];

    public IEnumerable<Neighbour> GetNeighbours(Cell cell) =>
        from direction in AllDirections
        let adjacentCellOrNull = AdjacentCellOrNull(cell, direction)
        where adjacentCellOrNull != null
        select new Neighbour(Cell: adjacentCellOrNull, Direction: direction);

    // Existing members ...
}

Next, we need to define the state space around which we will be walking. Earlier, when I defined the algorithm, I said:

As you go through the process, keep track of the following pieces of state:

• Which cell walls are present
• The current cell
• The path you took to get there
• Which cells have been visited

This translates into C# in a reasonably straightforward manner.

public record RecursiveBacktrackerState(
    Maze Maze,
    Cell CurrentCell,
    ImmutableStack<Cell> Path,
    ImmutableList<Cell> Visited);

There are two options for each step in the process; I've called them "proceed" (pick an unvisited neighbour and move to it) and "backtrack" (move back to the previous cell).

private static IDistribution<RecursiveBacktrackerState> ProceedDist(
    RecursiveBacktrackerState state,
    IDistribution<Neighbour> unvisitedNeighbourDist) =>
    from neighbour in unvisitedNeighbourDist
    select new RecursiveBacktrackerState(
        Maze: state.Maze.RemoveWall(state.CurrentCell, neighbour.Direction),
        CurrentCell: neighbour.Cell,
        Path: state.Path.Push(state.CurrentCell),
        Visited: state.Visited.Add(neighbour.Cell));

private static RecursiveBacktrackerState Backtrack(
    RecursiveBacktrackerState state) =>
    state with { Path = state.Path.Pop(out var cell), CurrentCell = cell };

Using the ImmutableStack class for the path makes it easy to implement the "backtrack" step.

In order to create a random walk, we need to define the initial state and the distribution of the next step given the current state. In our case, the initial state is actually random, so we need a distribution rather than a concrete value.

private static IDistribution<RecursiveBacktrackerState> InitialStateDist(
    Grid grid) =>
    from cell in UniformDistribution.Create(grid.Cells)
    select new RecursiveBacktrackerState(
        Maze: Maze.WithAllWalls(grid),
        CurrentCell: cell,
        Path: [],
        Visited: [cell]);

private static IDistribution<RecursiveBacktrackerState> NextStateDist(
    Grid grid, RecursiveBacktrackerState state)
{
    var unvisitedNeighbours = grid.GetNeighbours(state.CurrentCell)
        .Where(n => !state.Visited.Contains(n.Cell));
    return UniformDistribution.TryCreate(
            unvisitedNeighbours, out var unvisitedNeighbourDist) ?
        ProceedDist(state, unvisitedNeighbourDist) :
        Singleton.New(Backtrack(state));
}

Next, we need to define when to stop the process; otherwise we'll carry on forever!

private static bool StopIteration(RecursiveBacktrackerState state, Grid grid) => 
    AllCellsVisited(state, grid) && state.Path.IsEmpty;

private static bool AllCellsVisited(RecursiveBacktrackerState state, Grid grid) =>
    state.Visited.Count == grid.CellCount;

And then, finally, we can compose our building blocks to give us a distribution. As in previous posts, I've implemented one function to give us the history (so we can make an animation) and one function if we just want the maze at the end of it.

public static IDistribution<IReadOnlyList<RecursiveBacktrackerState>> HistoryDist(
    Grid grid) =>
    from initial in InitialStateDist(grid)
    from randomWalk in RandomWalk.New(initial, s => NextStateDist(grid, s))
    select randomWalk.TakeWhile(s => !StopIteration(s, grid)).ToReadOnly();

public static IDistribution<Maze> MazeDist(Grid grid) =>
    from history in HistoryDist(grid)
    select history.Last().Maze;

Results

To finish, I've generated a maze on a 25x25 grid, because why not?!

I've also updated the playground website with support for the Recursive Backtracker algorithm.

Up next

One thing you might have spotted is that, unlike the previous two algorithms, Recursive Backtracker doesn't rely on using a rectangular grid: all that matters is that we know which cells are neighbours. In the next post we'll investigate drawing mazes on more interesting-looking grids.