ProcGen Fun 1: Distributions

[List of posts | source code for this post]

Merry Christmas! 🎄

To start off, I've created a Visual Studio solution and two C# projects:

• ProcGenFun will contain the core code and will strictly follow functional programming principles.
• ProcGenFun.WinForms is a Windows Forms application which will enable us to visualise the results of our functional core. This project will contain some imperative code.

Distributions

In a previous post on this blog I introduced the concept of a distribution: a source of random values of a given type corresponding to some probability distribution. This abstraction is useful for expressing stochastic (i.e. non-deterministic) algorithms in a functional way.

public interface IDistribution<T>
{
    T Sample();
}

In this series I'll be using the NuGet package RandN, which declares a variant of this interface:

public interface IDistribution<T>
{
    T Sample<TRng>(TRng rng);
}

The difference here is the presence of a random number generator (RNG), which is passed into the Sample() method. This is actually quite useful for maintaining functional purity, because we can make sure that we never create an RNG within the functional core; instead it will be created in the impure WinForms project and passed in where needed.

(Aside: there's also a TrySample() method on this interface, which we will be largely ignoring during this series.)

Example

RandN comes with a handful of built-in distributions. A simple example is the uniform distribution; calling Uniform.New(0d, 1d) gives us a uniform distribution of doubles between 0 and 1.

Given a collection of samples from a distribution, we can make a histogram; this calculation is functional, so can go in the core project.

public static Histogram New(IEnumerable<double> values, double min, double max)
{
    const int bucketCount = 100;
    var buckets = new int[bucketCount];

    foreach (var value in values)
    {
        var bucketIndex = (int)(bucketCount * (value - min) / (max - min));
        if (0 <= bucketIndex && bucketIndex < bucketCount)
        {
            buckets[bucketIndex]++;
        }
    }

    var bucketWidth = (max - min) / bucketCount;

    return new Histogram(
        buckets
            .Select((count, index) => new HistogramBucket(
                Centre: min + bucketWidth * (index + 0.5),
                Count: count))
            .ToList(),
        bucketWidth);
}

Then in the WinForms project we can take a large number of samples, generate a histogram, and plot it.

private void DisplayHistogram()
{
    var rng = StandardRng.Create();
    var dist = Uniform.New(0d, 1d);

    var values = TakeSamples(dist, count: 100_000, rng);

    DisplayHistogram(values);
}

private static IEnumerable<T> TakeSamples<T, TRng>(
    IDistribution<T> dist, int count, TRng rng)
    where TRng : notnull, IRng
{
    for (int i = 0; i < count; i++)
    {
        yield return dist.Sample(rng);
    }
}

private void DisplayHistogram(IEnumerable<double> values)
{
    var histogram = Histogram.New(values, min: 0, max: 1);

    formsPlot.Reset();
    var barPlot = formsPlot.Plot.Add.Bars(
        histogram.Buckets.Select(b => b.Centre),
        histogram.Buckets.Select(b => b.Count));

    foreach (var bar in barPlot.Bars)
    {
        bar.Size = histogram.BucketWidth;
    }

    formsPlot.Refresh();
}

(I'm using another NuGet package, ScottPlot, to visualise the results.)

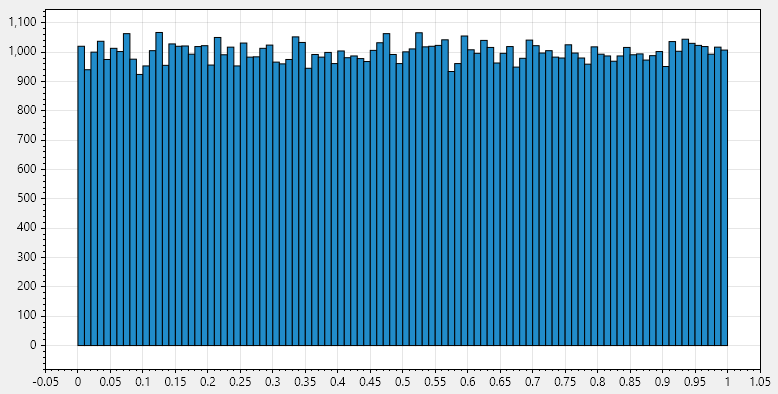
As you can see, we've got a broadly uniform spread of values between 0 and 1.

Conclusion

So far we've introduced an abstraction for randomness called a distribution. In post 2 we'll see how this abstraction allows us to compose random variables in a very functional way.